Blog

In my recent work on a greyhound racing prediction model, I’ve discovered an effective technique to not only increase the model’s performance but also stabilize it and reduce overfitting. This technique involves the use of multiple loss functions.

Traditionally, a single loss function is used to train a model. The model’s parameters are adjusted to minimize this loss, which is a measure of the difference between the model’s predictions and the actual data. However, in complex tasks like greyhound racing prediction, a single loss function may not capture all the nuances of the problem.

In my model, I used three different targets for the loss function, each focusing on a different aspect of the data:

1. Margin as a softmin tensor: The margin of victory in a race is a direct measure of how well each dog performed. By converting this margin to a softmin tensor, we transform the margins into a set of probabilities that sum to 1. The dog with the smallest margin (i.e., the winner) will have the highest probability. This target tensor directly relates to the outcome of the race and is crucial for the model to learn the relationship between the input features and the race outcome.

2. One-hot encoded win: This tensor represents the actual winner of the race. Each dog is represented by a binary value in the tensor, with the winner having a value of 1 and all others having a value of 0. This target tensor is essential for the model to learn to predict the categorical outcome of the race, i.e., which dog will win. It provides a clear and unambiguous target for the model to aim for.

3. Starting prices as probabilities: The starting prices in a race can be seen as the inverse of the market’s perceived probability of each dog winning. By converting these prices to probabilities, we create a target tensor that represents the collective opinion of the betting market. This tensor is important for the model to learn to take into account the same factors that bettors consider when placing their bets. It provides a different perspective on the race outcome, complementing the other two target tensors.

By training the model to predict all three target tensors, we enable it to learn different aspects of the problem and make more accurate and nuanced predictions. Each tensor contains unique information about the race outcome, and by combining them, we can create a model that is more robust and capable of generating more accurate probabilities.

#Single Target Loss
epoch_loss = criterion(output, y)
optimizer.zero_grad()
epoch_loss.mean().backward()
optimizer.step()

#Multiple Target Loss
epoch_loss = criterion(output, y)
epoch_loss_ohe = criterion(output, y_ohe)
epoch_loss_p = criterion(output_p, y_p)
optimizer.zero_grad()
(epoch_loss_p+epoch_loss_ohe+epoch_loss).mean().backward()
optimizer.step()

By training the model to minimize all three loss functions simultaneously, it learns to make predictions that are accurate in multiple respects. This not only improved the model’s performance on the main metric (loss to margin) but also made the model more stable and less prone to overfitting.

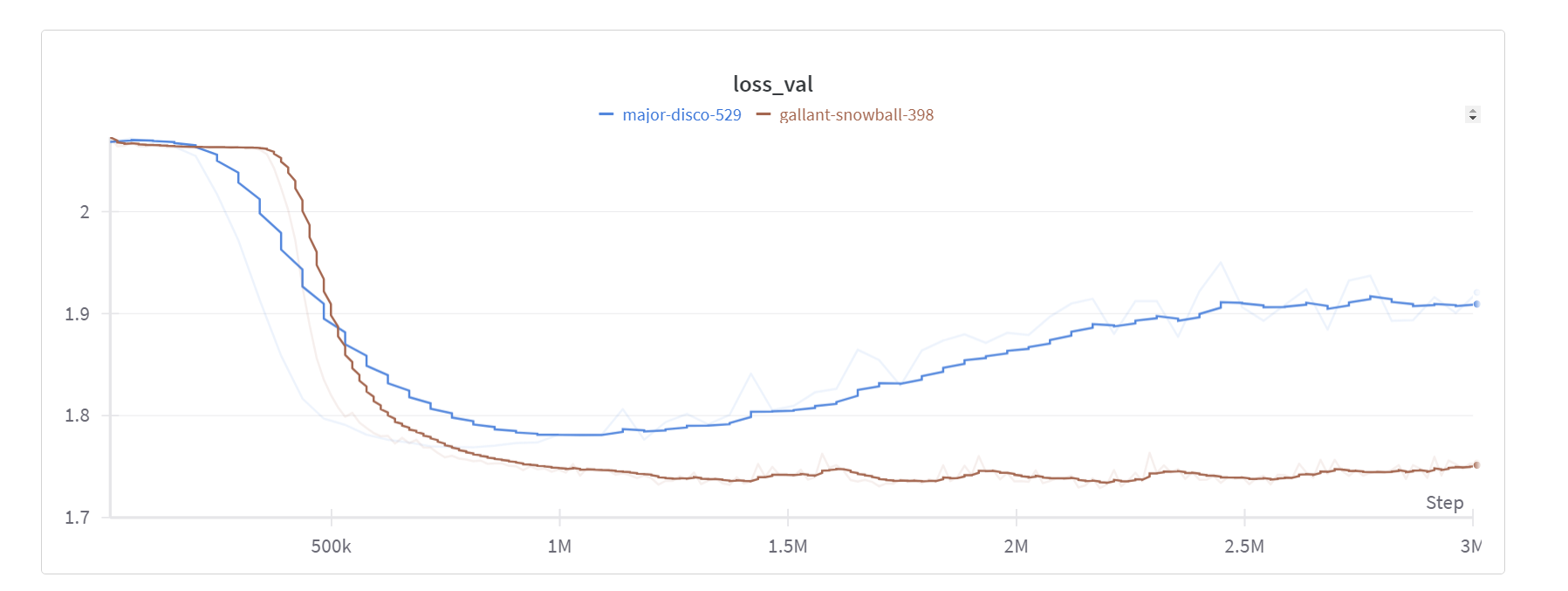
This also translates directly to an increase in validation accuracy on the prediction outcomes:

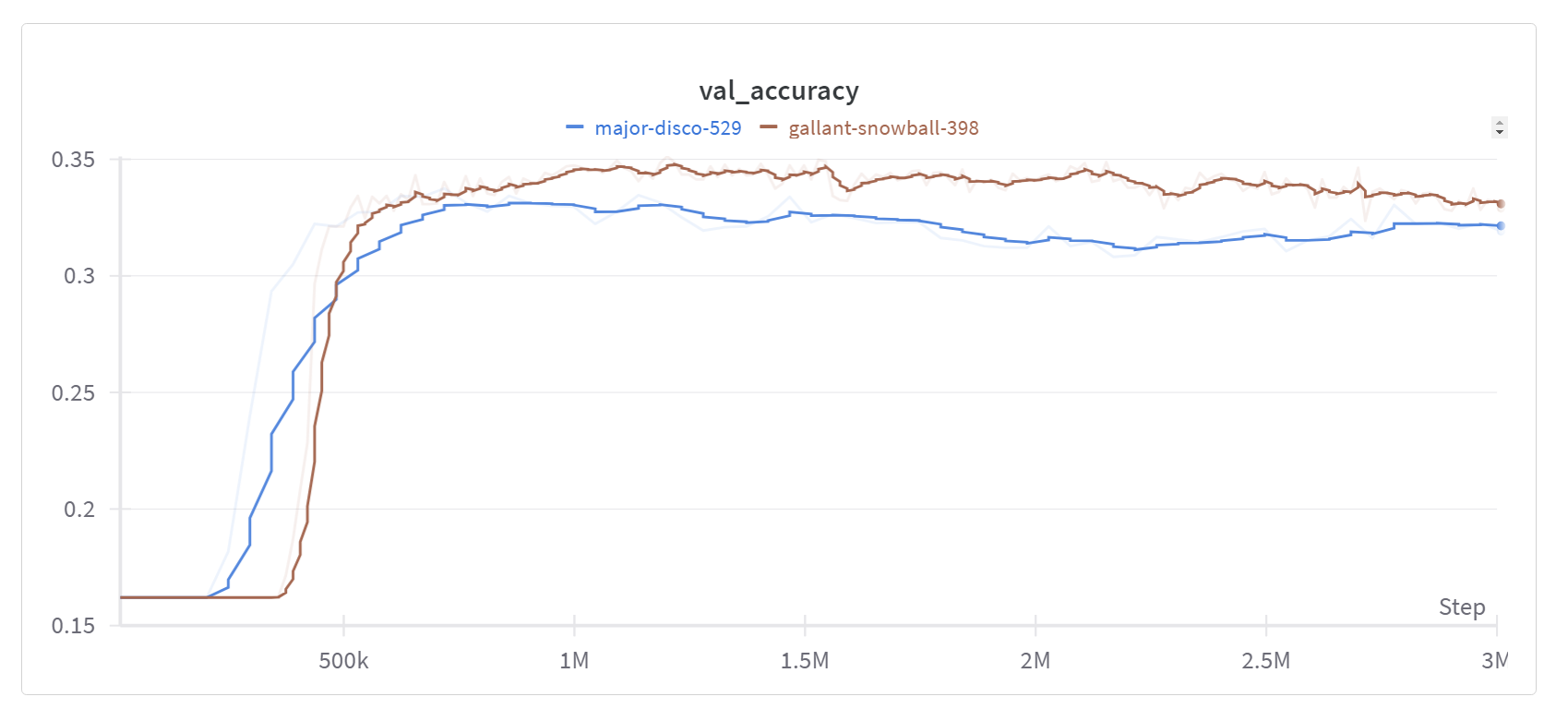
This approach of using multiple loss functions can be applied to other complex prediction tasks as well. It’s a powerful way to make your model learn from different perspectives and thus make more accurate and robust predictions.